982.20  Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one part__the line, which was so short a section of Earth arc (and the Earth's diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature's event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the "transcendentally irrational," ergo incommensurable, number pi ( Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one part__the line, which was so short a section of Earth arc (and the Earth's diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature's event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the "transcendentally irrational," ergo incommensurable, number pi (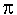 ), 3.14159 . . . ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres. ), 3.14159 . . . ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres. |
| 982.21  Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube's face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix's field-occurring-cube's diagonal edge has the value. of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency. Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube's face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix's field-occurring-cube's diagonal edge has the value. of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency. |
| 982.30  Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle's hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube's diagonaled face: half of four is two. Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle's hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube's diagonaled face: half of four is two. |
| 982.31  The square root of 2 = 1.414214, ergo, the length of each of the cube's edges is 1.414214. The sqrt(2)happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1:sqrt(2) = sqrt(2):2, which, solved, reads out as 1 : 1.414214 = 1.414214 : 2. The square root of 2 = 1.414214, ergo, the length of each of the cube's edges is 1.414214. The sqrt(2)happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1:sqrt(2) = sqrt(2):2, which, solved, reads out as 1 : 1.414214 = 1.414214 : 2. |
| 982.32  The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(23), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428. The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(23), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428. |
| 982.33  This is exploratorily noteworthy because this cube, when calculated in terms of man's conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value ofone__ergo, its volume would be one: 1 × 1 × 1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of sqrt(2), which equals 1.414214. Obviously, the use of the diagonal of the cube's face as the control length results in a much higher volume than when conventionally evaluated. This is exploratorily noteworthy because this cube, when calculated in terms of man's conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value ofone__ergo, its volume would be one: 1 × 1 × 1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of sqrt(2), which equals 1.414214. Obviously, the use of the diagonal of the cube's face as the control length results in a much higher volume than when conventionally evaluated. |
| 982.40  Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix__as most economically structured by nature__has a volume of three in synergetics' vector- edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one. Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix__as most economically structured by nature__has a volume of three in synergetics' vector- edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one. |
| 982.41  A necklace-edged cube has no structural integrity. A tension-linked, edge- strutted cube collapses. A necklace-edged cube has no structural integrity. A tension-linked, edge- strutted cube collapses. |
| 982.42  To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron's six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube's six square faces. To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron's six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube's six square faces. |
| 982.43  As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth-Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-comer angles of 45 degrees each; each of the 1/8th octahedron's asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, 2 + 1 = 3 = the volume of the cube. The cube is volume three where the tetrahedron's volume is one, and the octahedron's volume is four, and the cube's diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.) As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth-Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-comer angles of 45 degrees each; each of the 1/8th octahedron's asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, 2 + 1 = 3 = the volume of the cube. The cube is volume three where the tetrahedron's volume is one, and the octahedron's volume is four, and the cube's diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.) |
| 982.44  Therefore the edge of the cube = sqrt(1/2). Therefore the edge of the cube = sqrt(1/2). |
| 982.45  Humanity's conventional mensuration cube with a volume of one turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3. Humanity's conventional mensuration cube with a volume of one turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3.
3
---------
2.828428 | = 1.06066 |
|
| 982.46  To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant 1.06066. (See Chart 963.10.) To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant 1.06066. (See Chart 963.10.) |
| 982.47  Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the XYZ rectilinear-coordinate system__"cubism" is a convenient term__in which the cube's edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number- accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity. Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the XYZ rectilinear-coordinate system__"cubism" is a convenient term__in which the cube's edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number- accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity. |
| 982.48  All but the icosahedron and its "wife," the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron's wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron's 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible- tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604). All but the icosahedron and its "wife," the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron's wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron's 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible- tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604). |
| 982.50  Initial Four-Dimensional Modelability: The modelability of the XYZ coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube's edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical7 school curriculum. Initial Four-Dimensional Modelability: The modelability of the XYZ coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube's edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical7 school curriculum.
(Footnote 7: Energetical is in contradistinction to synergetical. Energetics employs isolation of special cases of our total experience, the better to discern unique behaviors of parts undiscernible and unmeasurable in total experience.) |
| 982.51  The XYZ cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and- circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari- sized cubism. The XYZ exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the XYZ system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two. The XYZ cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and- circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari- sized cubism. The XYZ exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the XYZ system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two. |
| 982.52  The synergetics coordinate system's initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics' isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability. The synergetics coordinate system's initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics' isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability. |
| 982.53  In the synergetics' four-, five-, and six-dimensionally coordinate system's operational field the linear increment modulatability and modelability is the isotropic vector matrix's vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonals__and not the edges__of the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics' exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the XYZ system's cubical values to the synergetics' values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron's edges and the cube's corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the-often odd-fractioned-edge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector- referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.) In the synergetics' four-, five-, and six-dimensionally coordinate system's operational field the linear increment modulatability and modelability is the isotropic vector matrix's vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonals__and not the edges__of the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics' exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the XYZ system's cubical values to the synergetics' values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron's edges and the cube's corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the-often odd-fractioned-edge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector- referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.) |
| 982.54  The mathematical constants for conversion of the linear, areal, and volumetric values of the XYZ system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows: The mathematical constants for conversion of the linear, areal, and volumetric values of the XYZ system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows:
- First Dimension: The first dimensional cube-edge-to-cube-face-diagonal vector conversion constant from XYZ to synergetics is as 1:1.060660.
- Second Dimension: The two-dimensional linear input of vector vs. cube-edged referenced, triangular vs. square area product identity is 1.0606602 = 1.125 = 1 1/8th = 9/8ths. The second-power value of the vector, 9/8, is in one-to-one correspondence with "congruence in modulo nine" arithmetic (see Secs. 1221.18 and 1221.20); ergo is congruent with wave-quanta modulation (see Secs. 1222 and 1223).
- Third Dimension: The three-dimensional of the cube-edge vs. vector-edged tetrahedron vs. cube volumetric identity is 1.0606603 = 1.192.
|
| 982.55  To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius l; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = 4/3 pi ( To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius l; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = 4/3 pi (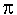 ) multiplied by the third power of the radius. Radius = 1. 13 = 1. l × 1.333 × 3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. VE sphere = 2 VE. ) multiplied by the third power of the radius. Radius = 1. 13 = 1. l × 1.333 × 3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. VE sphere = 2 VE. |
| 982.56  We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 LCD tetrahedral components of mild off- sizing are also truly of the same volumetric quanta value as the A and B Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 LCD asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40). We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 LCD tetrahedral components of mild off- sizing are also truly of the same volumetric quanta value as the A and B Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 LCD asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40). |
| 982.57  Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the F2 vector-equilibrium- vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 × 2 1/2 nuclear-sphere's inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics. Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the F2 vector-equilibrium- vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 × 2 1/2 nuclear-sphere's inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics. |
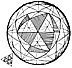
Fig. 982.58 | 982.58  Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral state__as witnessed in the jitterbugging (see Sec. 465) __did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the A or B Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 LCD Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron's triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium. Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral state__as witnessed in the jitterbugging (see Sec. 465) __did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the A or B Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 LCD Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron's triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium. |
| 982.59  We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron's and the vector equilibrium's prime number five topological identity. We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron's and the vector equilibrium's prime number five topological identity. |
| 982.60  Without any further developmental use of pi ( Without any further developmental use of pi (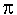 ) we may now state in relation to the isotropic vector matrix synergetic system, that: ) we may now state in relation to the isotropic vector matrix synergetic system, that:
| The volume of the sphere is a priori always quantitatively: |
| __ | 5F3 as volumetrically referenced to the regular tetrahedron (as volume = 1); or |
| __ | 120F3 as referenced to the A and B Quanta Modules. |
|
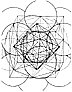
Fig. 982.61 | 982.61  There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 A and B Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially- rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state. There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 A and B Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially- rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state. |
| 982.61A  Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems: There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole- number, equilibrious state of the macro-micro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state. Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems: There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole- number, equilibrious state of the macro-micro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state. |
| 982.62  Table of Concentric, 12-Around-One, Closest-Packed Spheres, Each of a Tetra Volume of Five, i.e., 120 A and B Quanta Modules, Omniembracing Our Hierarchy of Nuclear Event Patternings. (See also Illus. 982.61 in drawings section.) Table of Concentric, 12-Around-One, Closest-Packed Spheres, Each of a Tetra Volume of Five, i.e., 120 A and B Quanta Modules, Omniembracing Our Hierarchy of Nuclear Event Patternings. (See also Illus. 982.61 in drawings section.)
| Symmetrical Form: | Tetra Volumes | A and B
Quanta Modules |
| F2 Sphere | 40 | 960 |
| F2 Cube | 24 | 576 |
| F2 Vector equilibrium | 20 | 480 |
| F0 Rhombic dodecahedron | 6 | 144 |
| F0 Sphere (nuclear) | 5 | 120 |
| F0 Octahedron | 4 | 96 |
| F0 Cube | 3 | 72 |
| F0 Vector equilibrium | 2½ | 60 |
| F0 Tetrahedron | 1 | 24 |
F0 Skew-aberrated,
disequilibrious icosahedron | 5 | 120 |
F2 Skew-aberrated,
disequilibrious icosahedron | 40 | 960 |
|
| 982.62A  Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised): Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised):
| Symmetrical Form: | Tetravolumes | A and B
Quanta Modules |
| F0 Tetrahedron | 1 | 24 |
| F0 Vector equilibrium | 2.5 | 60 |
| F0 Double-Tet cube | 3 | 72 |
| F0 Octahedron | 4 | 96 |
| F0 Rhombic triacontahedron* | 5+ | 120+ |
| F0 Rhombic dodecahedron | 6 | 144 |
| F2 Vector equilibrium | 20 | 480 |
| F2 Double-Tet cube | 24 | 576 |
* The spheric spin domain of the rhombic triacontahedron "sphere." |
| 982.63  Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere. Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere. |
| 982.64  The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin. (12 + 4 + 6 + 3 = 25) The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin. (12 + 4 + 6 + 3 = 25) |
| 982.65  Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state. Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state. |
| 982.70  Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of A and B Quanta Modules per tetrahedron is 24 (see Sec.942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 A and B Quanta Modules); that the common prime number fivetopological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologies__see Sec. 905, especially 905.55; that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstable__because equilibrious__and is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically. Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of A and B Quanta Modules per tetrahedron is 24 (see Sec.942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 A and B Quanta Modules); that the common prime number fivetopological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologies__see Sec. 905, especially 905.55; that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstable__because equilibrious__and is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically. |
| 982.71  The significance of this unified field as defining and embracing the minimum- maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus- concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius spheres__each of which four layers is uniquely related to that nucleus__with each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array: The significance of this unified field as defining and embracing the minimum- maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus- concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius spheres__each of which four layers is uniquely related to that nucleus__with each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array:
| __ | the unity-one-radiused sphere of volume five; |
| __ | the octahedron of volume four; |
| __ | the cube of volume three; |
| __ | the prime vector equilibrium of volume 2 l/2; and |
| __ | the two regular (positive and negative) tetrahedra of volume one each. |
This succession of 1, 2, 3, 4, 5, 6 rational volume relationships embraces the first four prime numbers 1, 2, 3, and 5. (See Illus. 982.61 in color section.) The volume-24 (tetra) cube is thelargest omnisymmetrical self-packing, allspace-filling polyhedron that exactly identifies the unique domain of the original 12-around-one, nuclear-initiating, closest packing of unit-radius spheres. The unit quantum leap of 1__going to 2__going to 3__going to 4__going to 5__going to 6, with no step greater than 1, suggests a unique relationship of this set of six with the sixness of degrees of freedom.8
(Footnote 8: For further suggestions of the relationship between the rhombic dodecahedron and the degrees of freedom see Sec. 426 537.10 954.47.) |
| 982.72  The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have three__easily predictable__relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron. The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have three__easily predictable__relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron. |
| 982.73  The one-quantum "leap" is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron's 4 and thence to the tetrahedron's 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest- packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: 6 - 5 = 1. The one-quantum "leap" is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron's 4 and thence to the tetrahedron's 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest- packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: 6 - 5 = 1. |
Copyright © 1997 Estate of R. Buckminster Fuller
http://www.rwgrayprojects.com/synergetics/s09/p8220.html
 Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one part__the line, which was so short a section of Earth arc (and the Earth's diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature's event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the "transcendentally irrational," ergo incommensurable, number pi (
Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one part__the line, which was so short a section of Earth arc (and the Earth's diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature's event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the "transcendentally irrational," ergo incommensurable, number pi (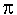 ), 3.14159 . . . ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres.
), 3.14159 . . . ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres. Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube's face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix's field-occurring-cube's diagonal edge has the value. of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency.
Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube's face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix's field-occurring-cube's diagonal edge has the value. of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency. Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle's hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube's diagonaled face: half of four is two.
Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle's hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube's diagonaled face: half of four is two. The square root of 2 = 1.414214, ergo, the length of each of the cube's edges is 1.414214. The sqrt(2)happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1:sqrt(2) = sqrt(2):2, which, solved, reads out as 1 : 1.414214 = 1.414214 : 2.
The square root of 2 = 1.414214, ergo, the length of each of the cube's edges is 1.414214. The sqrt(2)happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1:sqrt(2) = sqrt(2):2, which, solved, reads out as 1 : 1.414214 = 1.414214 : 2. The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(23), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428.
The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(23), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428. This is exploratorily noteworthy because this cube, when calculated in terms of man's conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value ofone__ergo, its volume would be one: 1 × 1 × 1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of sqrt(2), which equals 1.414214. Obviously, the use of the diagonal of the cube's face as the control length results in a much higher volume than when conventionally evaluated.
This is exploratorily noteworthy because this cube, when calculated in terms of man's conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value ofone__ergo, its volume would be one: 1 × 1 × 1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of sqrt(2), which equals 1.414214. Obviously, the use of the diagonal of the cube's face as the control length results in a much higher volume than when conventionally evaluated. Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix__as most economically structured by nature__has a volume of three in synergetics' vector- edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one.
Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix__as most economically structured by nature__has a volume of three in synergetics' vector- edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one. A necklace-edged cube has no structural integrity. A tension-linked, edge- strutted cube collapses.
A necklace-edged cube has no structural integrity. A tension-linked, edge- strutted cube collapses. To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron's six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube's six square faces.
To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron's six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube's six square faces. As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth-Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-comer angles of 45 degrees each; each of the 1/8th octahedron's asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, 2 + 1 = 3 = the volume of the cube. The cube is volume three where the tetrahedron's volume is one, and the octahedron's volume is four, and the cube's diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.)
As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth-Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-comer angles of 45 degrees each; each of the 1/8th octahedron's asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, 2 + 1 = 3 = the volume of the cube. The cube is volume three where the tetrahedron's volume is one, and the octahedron's volume is four, and the cube's diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.) Therefore the edge of the cube = sqrt(1/2).
Therefore the edge of the cube = sqrt(1/2). Humanity's conventional mensuration cube with a volume of one turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3.
Humanity's conventional mensuration cube with a volume of one turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3. To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant 1.06066. (See Chart 963.10.)
To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant 1.06066. (See Chart 963.10.) Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the XYZ rectilinear-coordinate system__"cubism" is a convenient term__in which the cube's edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number- accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity.
Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the XYZ rectilinear-coordinate system__"cubism" is a convenient term__in which the cube's edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number- accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity. All but the icosahedron and its "wife," the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron's wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron's 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible- tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604).
All but the icosahedron and its "wife," the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron's wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron's 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible- tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604). Initial Four-Dimensional Modelability: The modelability of the XYZ coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube's edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical7 school curriculum.
Initial Four-Dimensional Modelability: The modelability of the XYZ coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube's edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical7 school curriculum. The XYZ cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and- circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari- sized cubism. The XYZ exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the XYZ system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two.
The XYZ cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and- circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari- sized cubism. The XYZ exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the XYZ system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two. The synergetics coordinate system's initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics' isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability.
The synergetics coordinate system's initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics' isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability. In the synergetics' four-, five-, and six-dimensionally coordinate system's operational field the linear increment modulatability and modelability is the isotropic vector matrix's vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonals__and not the edges__of the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics' exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the XYZ system's cubical values to the synergetics' values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron's edges and the cube's corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the-often odd-fractioned-edge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector- referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.)
In the synergetics' four-, five-, and six-dimensionally coordinate system's operational field the linear increment modulatability and modelability is the isotropic vector matrix's vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonals__and not the edges__of the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics' exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the XYZ system's cubical values to the synergetics' values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron's edges and the cube's corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the-often odd-fractioned-edge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector- referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.) The mathematical constants for conversion of the linear, areal, and volumetric values of the XYZ system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows:
The mathematical constants for conversion of the linear, areal, and volumetric values of the XYZ system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows: To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius l; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = 4/3 pi (
To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius l; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = 4/3 pi (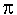 ) multiplied by the third power of the radius. Radius = 1. 13 = 1. l × 1.333 × 3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. VE sphere = 2 VE.
) multiplied by the third power of the radius. Radius = 1. 13 = 1. l × 1.333 × 3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. VE sphere = 2 VE. We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 LCD tetrahedral components of mild off- sizing are also truly of the same volumetric quanta value as the A and B Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 LCD asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40).
We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 LCD tetrahedral components of mild off- sizing are also truly of the same volumetric quanta value as the A and B Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 LCD asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40). Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the F2 vector-equilibrium- vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 × 2 1/2 nuclear-sphere's inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics.
Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the F2 vector-equilibrium- vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 × 2 1/2 nuclear-sphere's inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics.
 Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral state__as witnessed in the jitterbugging (see Sec. 465) __did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the A or B Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 LCD Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron's triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium.
Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral state__as witnessed in the jitterbugging (see Sec. 465) __did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the A or B Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 LCD Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron's triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium. We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron's and the vector equilibrium's prime number five topological identity.
We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron's and the vector equilibrium's prime number five topological identity. Without any further developmental use of pi (
Without any further developmental use of pi ( ) we may now state in relation to the isotropic vector matrix synergetic system, that:
) we may now state in relation to the isotropic vector matrix synergetic system, that:
 There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 A and B Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially- rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state.
There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 A and B Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially- rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state. Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems: There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole- number, equilibrious state of the macro-micro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state.
Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems: There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole- number, equilibrious state of the macro-micro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state. Table of Concentric, 12-Around-One, Closest-Packed Spheres, Each of a Tetra Volume of Five, i.e., 120 A and B Quanta Modules, Omniembracing Our Hierarchy of Nuclear Event Patternings. (See also Illus. 982.61 in drawings section.)
Table of Concentric, 12-Around-One, Closest-Packed Spheres, Each of a Tetra Volume of Five, i.e., 120 A and B Quanta Modules, Omniembracing Our Hierarchy of Nuclear Event Patternings. (See also Illus. 982.61 in drawings section.) Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised):
Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised): Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere.
Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere. The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin. (12 + 4 + 6 + 3 = 25)
The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin. (12 + 4 + 6 + 3 = 25) Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state.
Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state. Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of A and B Quanta Modules per tetrahedron is 24 (see Sec.942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 A and B Quanta Modules); that the common prime number fivetopological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologies__see Sec. 905, especially 905.55; that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstable__because equilibrious__and is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically.
Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of A and B Quanta Modules per tetrahedron is 24 (see Sec.942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 A and B Quanta Modules); that the common prime number fivetopological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologies__see Sec. 905, especially 905.55; that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstable__because equilibrious__and is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically. The significance of this unified field as defining and embracing the minimum- maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus- concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius spheres__each of which four layers is uniquely related to that nucleus__with each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array:
The significance of this unified field as defining and embracing the minimum- maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus- concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius spheres__each of which four layers is uniquely related to that nucleus__with each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array: The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have three__easily predictable__relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron.
The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have three__easily predictable__relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron. The one-quantum "leap" is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron's 4 and thence to the tetrahedron's 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest- packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: 6 - 5 = 1.
The one-quantum "leap" is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron's 4 and thence to the tetrahedron's 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest- packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: 6 - 5 = 1.
