WRITING MATHEMATICAL EXPRESSIONS IN PLAIN TEXT - EXAMPLES AND CAUTIONS

Mathematical expressions can be typed online in a number of ways including plain text, ASCII codes, HTML tags, or using an equation editor (see Writing Mathematical Notation Online for overview). The most common way is to write expressions horizontally in plain text, but you have to format the expressions carefully using appropriately placed parentheses and accurate notation. This document provides examples and important cautions for writing mathematical expressions in plain text.
Section 1. How to Write Exponents
Just as on a graphing calculator, when writing in plain text the caret key ^ (above the 6 on a qwerty keyboard) means that an exponent follows. For example
2x
would be written as x^2.
Example 1a.
234xy
would be written as 4 x^2 y^3 or for added clarity with the multiplication mark as 4*x^2*y^3.
Example 1b. With more than one item in the exponent you must enclose the entire exponent in parentheses to indicate exactly what is in the power.
2nx
must be written as x^(2n) and NOT as x^2n. Writing x^2n means
2xn
Example 1c. When using the quotient rule of exponents you often have to perform subtraction within an exponent. In such cases you must enclose the entire exponent in parentheses to indicate exactly what is in the power. The middle step of
55232xxxx
must be written as x^(5-2) and NOT as x^5-2 which means
52x
Example 1d. You must enclose fractional exponents in parentheses to indicate that the entire fraction is in the power.
23x
must be written as x^(2/3) and NOT as x^2/3. Writing x^2/3 means
23x
Section 2. How to Write Repeating Decimals
There is no over-strike bar on your keyboard, so the only way to write a repeating decimal in plain text is to write several repetitions of the repeating numbers followed by an ellipsis (dot dot dot).
Example 2.
1.23
would be written as 1.2323232323…
Section 3. How to Write Absolute Value Bars
On the right of your keyboard, usually above the backslash, is a mark that looks like a vertical dash above another vertical dash. It produces a single vertical bar |. Use it to produce absolute value bars.
Example 3.
23x
could be written as 2-|x-3|.
Section 4. How to Write Inequalities
The less than and greater than keys are on your keyboard. To type “less than or equal to” or “greater than or equal to” type the original inequality, select it, and underline it to produce < or >. Alternatively use an ASCII code to produce these symbols (ALT+243 and ALT+242). On a MAC computer hold down ALT while typing the original inequality and it will automatically create ≤ or ≥.
Example 4. 30 is less than or equal to x could be written as 30 ≤ x.
Section 5. How to Write Fractions
When writing rational expressions (fractions) horizontally USE PARENTHESES. When the numerator contains more than one item, you MUST have parentheses around the entire numerator. When the denominator contains more than one item, you MUST have parentheses around the entire denominator.
Example 5a.
23xx
would be written horizontally as (2x)/(x-3).
Parentheses must enclose the entire numerator and parentheses must enclose the entire denominator to indicate that the entire 2x is divided by the entire x-3. I can’t stress enough how important this is!
If you neglect the parentheses and write 2x/x-3 then, by order of operations, this means
23xx
, a completely different expression.
Example 5b.
32x
must be written as 3/(x-2) and NOT as 3/x+2. Writing 3/x+2 means
32x.
Example 5c.
32x
must be written as (x+3)/2 and NOT as x+3/2. Writing x+3/2 means
32x
Example 5d.
(1)(2)(3)(4)xxxx
must be written as [(x-1)(x-2)] / [(x-3)(x-4)] and NOT as (x-1)(x-2)/(x-3)(x-4). Note the extra set of grouping symbols (I like to use square brackets) around the entire numerator and around the entire denominator. Believe it or not, by order of operations, writing (x-1)(x-2)/(x-3)(x-4) means
(1)(2)(4)(3)xxxx
, ugh! See how messed up things can get if you neglect to include the parentheses to clearly indicate what expression is in the numerator and what expression is in the denominator?
Example 5e. This common “neglected parentheses” notation error only occurs when you are typing the problem horizontally. Instead you could write the fraction vertically. For example, instead of writing
23xx
horizontally as (2x)/(x-3) you could write the fraction vertically (see below) and then you don't need the parentheses because it is clear exactly what is being divided by what. 2x_ x – 3 To produce this fraction type the numerator, type the denominator in the next line down (use SHIFT+ENTER), highlight the numerator, and click the underline key U to form the fraction bar. Voila!
Section 6. How to Write Radicals
You can use “sqrt” for square root, “cubert” or “3RT” for cube root, “fourthrt” or “4RT” for fourth root, etc. No matter what the index of the radical is, be sure to enclose the entire radicand in parentheses to indicate exactly what is in the radical.
Example 6a.
3x
would be written as sqrt(x+3).
Don’t forget the parentheses! Do NOT write sqrt x+3 as this means
3x
, a very different expression. The same caution holds if you use ASCII codes to create the radical symbol (ALT+251 will create √). You must write √(x+3) not √x+3. Writing √(x+3) means the square root of the entire x+3, i.e. x  3 , but √x+3 means only the x is under the radical, i.e. x  3 . Similarly √5x means
5x
with only the 5 under the radical, but if you want
5x
you must instead write √(5x).
Example 6b.
23x
could be written as cubert(x^2) or as 3RT(x^2) or using fractional exponents as x^(2/3).
Do NOT write as 3sqrt(x^2) nor as 3√x^2 as these both mean “3 times a square root” not “cube root”. The
symbol can only be used for square roots, not higher roots.
It is a bit of a cheat, but here is a shortcut for higher index radicals. Using ASCII codes to create the radical sign type 3√(x²) then select the 3 and hit the superscript key in the discussion board message menu (the icon looks like x²) so that the 3 turns into a little 3 index as in ³√x which is recognizable as the cube root of x.
Example 6c.
321x
could be written as cubert(2x-1) or as 3RT(2x-1) or using fractional exponents as (2x-1)^(1/3).
Example 6d.
45x
could be written as fourthrt(x/5) or as 4RT(x/5) or as (x/5)^(1/4).
Example 6e.
52xy
could be written as 2x*fifthrt(y) or as 2x*5RT(y) or as 2xy^(1/5).
Example 6f. The quadratic formula
242bbacxa
could be written as x = [-b +/- sqrt(b^2 – 4ac)] / [2a] I know it’s ugly, but accurate! Using ASCII codes you could clean it up a bit: x = [-b ± √(b^2 – 4ac)] / [2a].
Section 7. How to Write Logarithms
Natural and common logarithms can easily be typed as is. It is only logarithms with a specific base displayed that require special formatting. No matter what type of logarithmic function, be sure to enclose the entire argument in parentheses to indicate exactly what is in the logarithm.
Example 7.
3log(2)x
could be typed initially as LOG3(x-2), then select the 3 and click the subscript key in the discussion board message menu (the icon looks like2x) to create LOG3(x-2). Using capital letters for the logarithm isn’t necessary but does intensify the smallness of the base.
Section 8. How to Write Trigonometric Expressions
Example 8a. Some Greek letters can be typed using ASCII codes (or HTML tags if you are familiar with HTML programming). Otherwise, I recommend that you use acceptable alternatives. For instance,
cos
can be written as cos(theta), cos(t), or cosT.
sin(2)
can be written as sin(2 alpha), sin(2a), or sin2A.
Example 8b.
2cossin
could be written as 2cos(t)sin(t) or as 2cosTsinT.
Example 8c.
sincos
could be written as sin(t)/cos(t) or as sinT/cosT.
Example 8d.
2sin
could be written as (sin(t))^2 or as (sinT)^2.
Do NOT write sinT^2 which might be interpreted
2sinT
, nor sin^2T which looks like the nonsensical
2sinT
Example 8e.
1cosx
is best written as arccos(x).
Do NOT write cos^-1(x) because the -1 is not an exponent.
Example 8f. Common trig symbols include the angle symbol and the degree mark. For the angle symbol personally I use HTML tags, but in plain text you can just use words such as writing ∠B as “angle B”. To produce the degree mark (which is vitally important to include on every angle that is in degrees so as to not confuse it with radians) using an ASCII code is an easy way (ALT+0176 will create ° ). Or you can click the superscript key in the discussion board message menu (the icon looks like x2) then put a little oh for the power. Or you can just use words such as writing 30° as “30 degs”.
Section 9. How to Write Calculus (Limits, Derivatives, and Integrals)
Using an equation editor to type calculus expressions online is preferred, but occasionally a quick plain text message is appropriate so here are examples of typing limits, derivatives, and integrals.
Example 9a.
0sinlimxxx
can be written in words as “the limit of (sinx)/x as x->0” or by writing “lim x->0 (sinx))/x” preferably with x->0 as a subscript so it looks like “limx->0(sinx)/x”.
Example 9b.
2lndxdx
can be written as d/dx (ln x^2).
Example 9c. If evaluating the derivative at a specific value such as
21lnedxdx
you can use the horizontal “evaluate at” bar which is, on a standard keyboard, on the right side above the \ symbol and looks like two vertical lines but types as |. So this expression could be written as “d/dx (ln x^2)|x=1 to x=e” or use more words such as “d/dx (ln x^2) evaluated from x=1 to x=e”.
Example 9d.
sinxexdx
can be written using INT for “the integral of” as in “INT(e^x*sin(x))dx”. Note that the integral symbol can be typed using HTML tags if you are familiar with HTML programming.
Example 9e. If evaluating a definite integral, more words must be used or again the horizontal “evaluate at” bar. For instance
1sinxexdx
could be written as “INT(e^x*sin(x))dx|x=1 to x=pi” or “INT(e^x*sin(x))dx evaluated from x=1 to x=pi”.
Example 9f.
512kk
can be written as “SUM(1/(k-2))|k=5 to k=infinity” or “SUM(1/(k-2)) from k=5 to k=infinity”. Note that the summation sign and the infinity sign can be written using ASCII codes or HTML if you prefer.
Copyright © 2009 Sally J. Keely. Writing Math Plain Text.docx
All Rights Reserved. revised 2012-10-22
http://www.integreat.ca/OL/docs/WritingMathPlainText.pdf 

ETHICAL DONATORS AND COMMUNITY MEMBERS REQUIRED, TO FILL THIS SPACE WITH YOUR POLITICAL SLOGANS, ADVERTISING OFFERS,WEBSITE DETAILS, CHARITY REQUESTS, LECTURE OPPORTUNITIES, EDUCATIONAL WORKSHOPS, SPIRITUAL AND/OR HEALTH ENLIGHTENMENT COURSES.

AS AN IMPORTANT MEMBER OF THE GLOBAL INDEPENDENT MEDIA COMMUNITY, MIKIVERSE SCIENCE HONOURABLY REQUESTS YOUR HELP TO KEEP YOUR NEWS, DIVERSE, AND FREE OF CORPORATE, GOVERNMENT SPIN AND CONTROL. FOR MORE INFORMATION ON HOW YOU MAY ASSIST, PLEASE CONTACT: themikiverse@gmail.com

THE HARVARD YARD

ETHICAL DONATORS AND COMMUNITY MEMBERS REQUIRED, TO FILL THIS SPACE WITH YOUR POLITICAL SLOGANS, ADVERTISING OFFERS,WEBSITE DETAILS, CHARITY REQUESTS, LECTURE OPPORTUNITIES, EDUCATIONAL WORKSHOPS, SPIRITUAL AND/OR HEALTH ENLIGHTENMENT COURSES.

AS AN IMPORTANT MEMBER OF THE GLOBAL INDEPENDENT MEDIA COMMUNITY, MIKIVERSE SCIENCE HONOURABLY REQUESTS YOUR HELP TO KEEP YOUR NEWS, DIVERSE, AND FREE OF CORPORATE, GOVERNMENT SPIN AND CONTROL. FOR MORE INFORMATION ON HOW YOU MAY ASSIST, PLEASE CONTACT: themikiverse@gmail.com

JOHANNES KEPLER-NEW ASTRONOMY-PART 1, ON RELATIONSHIPS OF HYPOTHESES-CHAPTER ONE, OBSERVING THE HEAVENS

The testimony of the ages confirms that the motions of the planets are orbicular. It is an immediate presumption of reason, reflected in experience, that their gyrations are perfect circles. For among figures it is circles, and among bodies the heavens, that are considered the most perfect. However, when experience is seen to teach something different to those who pay careful attention, namely, that the planets deviate from a simple circular path, it gives rise to a powerful sense of wonder, which at length drives men to look into causes. (p.115)

---

The Starry Vault

Our earth, which we are standing on, is the huge blue sphere, and the blue circle around it is the horizon, the limits of our sight. Imagine you are on your back, looking up. This is a live view of the night sky from an undisclosed location. Watch it carefully!

Actually, this picture doesn't move at all, but that's what stargazing is like! You don't see a particular star move any more than you can see the hour-hand on a watch moving, yet the change happens. Let's say you look up again in an hour. Here's what you'd see:

What happened now? Take another look a while later, and you'll see this:

---

The stars all seem to move in the sky. Doing this for an entire night until the sun comes up and ruins your view, you observe this (noting one particularly bright, redish star that stands out to you):

Do certain stars move faster than others? It seems that each star moves in its own particular circle, and there seems to be a spot where the star doesn't move at all. This spot that doesn't seem to move during the night, but around which the other stars move, acts like the end of a large pole, so we can call the star located there the pole-star. Now we have some directions! It also seems that the sun rises and sets not in the pole direction, or opposite it, but in between its direction and the opposite. We can name these directions: the pole-star direction is North (unless you're in Australia and see a certain cross that seems to rotate while maintaining the same position and call this pole South), its opposite is South, and the directions of the rising and setting of the sun East and West, respectively.

First and Second Motions

Around a dozen or so days later, you see the moon every night as well. Let's take a few nights and spend them watching the sky. Although you may find it easier to look at two at once to compare them, how would you do so without a computer animation? The motion would only be in your mind, or, expressed by your mind in a drawing.

First night


Next night


Last night
What did you discover? How high was the moon in the sky at sun-down on the three days? Among which stars is it found? Does everything in the sky move at the same speed? Which moves faster: the stars or the moon? You have now discovered the difference between the First Motion and the Second Motion: the first motion presenting itself to the mind of all the stars, including the moon, and the second motion, seen only through thought and comparison, of the particular heavenly bodies moving against the stars:

The first motion is that of the whole heaven and of all its stars from east past the meridian to the west... The second motions are those of the individual planets from the west to the east. (p.115)

Taking more care in the observations, it is noticed that the sun, too, moves more slowly than the stars. The stars are more advanced at each sunset. Here are a week's worth of sunsets, as they appear to the animating mind (not the eyes):

A week of sunsets

This first adumbration of astronomy explains no causes, but consists solely of the experience of the eyes, extremely slowly acquired. (p.117)

At this same time of year, while the red star rises near sunset, and is particularly bright (do other stars change their brightess during the year?), we can observe it at its peak, around the middle of the night. By using our mind to remove the daily motion of the heavens, we can focus our powers of reason upon the single star's second motion: this brings out more problems! Let's combine a couple of weeks of observations, creating the following animation in our minds:

This bright star, which, like the sun, usually was slower than the stars, being left behind them every night in the westward motion, reaches a time of staying even with them, and then, contrary to its usual motion, moves faster to the west than the fixed stars, before again stopping and resuming its eastward motion... This

"...gives rise to a powerful sense of wonder, which at length drives men to look into causes."

Retrograde

A paradox:

It was apparent that the three superior planets, Saturn, Jupiter, and Mars, attune their motions to their proximity to the sun. For when the sun approaches them they move forward and are swifter than usual, and when the sun comes to the sign opposite the planets they retrace with crablike steps the road they have just covered. (p.118)

(Click here for a visualization of how Ptolemy and Brahe conceived this occuring.) That this retrogression, or backwards-motion, occurs always when the sun is opposite these planets ("wanderers" in Greek), is peculiar, for they do not make their path through the stars in the same time as the sun. Our bright red star Mars, for example, moves through the stars and regains its original position in a little less than two years, although the exact amount of time changes from cycle to cycle, owing to the influence of its proximity to the sun on its path. These two, different, but interacting tendencies among the second motion of a particular planet, are known as the first inequality (its motion through the stars) and the second inequality (the relationship of its proximity to the sun on its motion).
In order to study the first inequality by itself, we'll have to remove the influence of the second inequality.

But in order to separate the second inequality from this first one, they could proceed no otherwise than by considering the planets on those nights at whose beginning they rise while the sun is setting, which thence were called akronychioi, or night rising... [A]t the very moments of conjuunction with and opposition to the sun they are traversing their own true and proper positions. But since they cannot be seen when in conjunction with the sun, only the opposition to the sun remains as suitable for this purpose. (p.120)

Retrograde occuring at opposition. The light blue spot is the location opposite the sun -- the Earth's zodiacal position. (Note the extreme latitude at opposition. The blue line at the bottom of the animation is the ecliptic -- the path that the sun traces against the stars, and the average latitude of Mars.)
Keep reading for mean and apparent oppositions!

---

You can click here for a draft, 3D version of the spherical animation.
http://science.larouchepac.com/kepler/newastronomy/ 

ETHICAL DONATORS AND COMMUNITY MEMBERS REQUIRED, TO FILL THIS SPACE WITH YOUR POLITICAL SLOGANS, ADVERTISING OFFERS,WEBSITE DETAILS, CHARITY REQUESTS, LECTURE OPPORTUNITIES, EDUCATIONAL WORKSHOPS, SPIRITUAL AND/OR HEALTH ENLIGHTENMENT COURSES.

AS AN IMPORTANT MEMBER OF THE GLOBAL INDEPENDENT MEDIA COMMUNITY, MIKIVERSE SCIENCE HONOURABLY REQUESTS YOUR HELP TO KEEP YOUR NEWS, DIVERSE, AND FREE OF CORPORATE, GOVERNMENT SPIN AND CONTROL. FOR MORE INFORMATION ON HOW YOU MAY ASSIST, PLEASE CONTACT: themikiverse@gmail.com

A URINE POWERED GENERATOR: MAKER FAIRE AFRICA

Posted on Tuesday, November 6, 2012 

Possibly one of the more unexpected products at Maker Faire Africa this year in Lagos is a urine powered generator, created by four girls. The girls are Duro-Aina Adebola (14), Akindele Abiola (14), Faleke Oluwatoyin (14) and Bello Eniola (15).
1 Liter of urine gives you 6 hours of electricity.

The system works like this:

• Urine is put into an electrolytic cell, which separates out the hydrogen.
• The hydrogen goes into a water filter for purification, which then gets pushed into the gas cylinder.
• The gas cylinder pushes hydrogen into a cylinder of liquid borax, which is used to remove the moisture from the hydrogen gas.
• This purified hydrogen gas is pushed into the generator.

Along the whole way there are one-way valves for security, but let’s be honest that this is something of an explosive device…

http://makerfaireafrica.com/2012/11/06/a-urine-powered-generator/

NASA RESEARCHER FINDS HIDDEN PORTALS IN EARTH’S MAGNETOSPHERE

By Susanne Posel,
Jack Scudder and his team of researchers at the University of Iowa have found “X-points” in the Earth’s magnetosphere; a magnetic field naturally generated by the Earth. The magnetosphere is a protective magnetic buffer between the sun’s radiation and solar winds and the earth’s atmosphere. It also holds the true northerly direction found with magnetic compasses.
NASA satellites have revealed “portals” in the magnetosphere which Scudder explains are: “places where the magnetic field of Earth connects to the magnetic field of the Sun, creating an uninterrupted path leading from our own planet to the sun’s atmosphere 93 million miles away.”
These openings allow charged solar particles to be conducted in the planet’s upper atmosphere. The effects of this phenomenon are seen as the aurorae displays and geomagnetic storms we experience.
David Sibeck, professor with the Goddard Spacelight Center explained in 2008 that “ten years ago I was pretty sure they didn’t exist, but now the evidence is incontrovertible.”
X-points , which have been seen from NASA spacecraft, are now the focal point of future missions of study to assert more detail. While they are considered elusive, temporary structures which can form and vanish unpredictably, NASA hopes to be lucky enough to “stumble” upon them once more to analyze data derived from their appearance.
Scudder believes he has found a way to detect them by examining decades old NASA data from the Polar spacecraft which was launched in 1996. It remains in orbit around the Earth despite it’s decommission in 2008. Scudder says: “Using Polar data, we have found five simple combinations of magnetic field and energetic particle measurements that tell us when we’ve come across an X-point or an electron diffusion region. A single spacecraft, properly instrumented, can make these measurements.”
X-points form when mingling lines of magnetic force from the sun and Earth and join to create the actual portals. The term “X-points’ are where the criss-cross manifests.
Using Scudder’s detection system, the time utilized to locate X-points would be greatly diminished. Without it, the location process could take up to a year or more. Finding X-points now should be done with ease and nearly immediately.
NASA will launch a research study called the Magnetospheric Multiscale Mission (MMS)in 2014. Fours spacecraft used for MMS will use energetic particle detectors and magnetic sensors and spread out in the planet’s magnetosphere and encircle the portals to observe how they work.

http://myscienceacademy.org/2012/10/14/nasa-researcher-finds-hidden-portals-in-earths-magnetosphere/

TWINKLE, TWINKLE, ELECTRIC STAR

By Liam Scheff
theintelhub.com
June 8, 2012
In this excerpt from Liam Scheff’s “Official Stories”,” we’ll see how even NASA is getting it wrong. Yes, even astronomy, the “queen of the sciences,” is locked up in the same fictions that dog the medical sciences and the political landscape. If “official stories exist to protect officials,” what’s the official story of outer space? The answer: Big Bang “theory” and stars as “nuclear bombs in space.” Are either true? Let’s have a look beneath the surface…
The Official Story: Stars are nuclear explosions in space.
The Lone Gunman: Gravity.
The Magic Bullet: No one really has one yet.
When humans first saw stars, they felt what we all feel. It even has its own word: starstruck. We marvel, we beam, our pupils open wide to let in the twinkling light. We feel that someone somewhere out there is looking at us, looking at them. It’s a wonderful, transcendent feeling.
When natural philosophers first set out to make a model of stars, they looked at fire on Earth – campfires, coal fires, forest and oil fires – and decided that stars were the same thing, only way up there. When humans forced the atomic attractions apart and exploded those monstrous bombs, they rethought the “campfire in space” model and called stars “nuclear furnaces.” But neither campfires nor nuclear explosions relate to what data-collecting telescopes have told us about the Sun.
First, where is a campfire hottest: above the fire, or in the burning coals? Don’t try to figure it out with bare hands. The answer is, in the source of the energy for the flame – the burning coals.
Where is a nuclear explosion hottest: in the center, at ground zero or a hundred miles away? Visitors to Hiroshima and Nagasaki know the answer. All fires and explosions are hottest and most violent at their source of energetic origin – the center. Where would you expect a star to be hottest: In the center, on the surface, or high above in its upper atmosphere?
The surface of the Sun is about 5,700 degrees Celsius. That’s almost four times the melting point of steel – which is hot. But, it’s surprisingly cool when you think that it warms our little planet, 93 million miles away.
So, how hot is the center? No one knows – no one’s been to or seen the center of a star, but sunspots do give a shallow view beneath the surface. Sunspots remain a mystery to the mainstream. They are like moving craters in the Sun, depressions in the surface revealing a glimpse of what’s underneath. And what’s underneath is cooler, by thousands of degrees.
This isn’t how a nuclear explosion works. But it makes sense to plasma physicists, who see sunspots as points where the strongest current flow from the galaxy punches holes in the bright surface, pushing back the sea of burning arc-plasma tornadoes that make up the surface of the Sun and revealing a sub-surface thousands of degrees cooler.
Does it make sense for a nuclear explosion? The mainstream has no explanation for this, just some impromptu hand-waving about disconnected magnetic fields (without understanding their electrical nature) with the obligatory catchphrase: “Another anomaly – send more money for research!”
But 10,000 kilometers above the surface, in the Sun’s atmosphere, called the corona, for “crown,” the temperature heats up. Not to thousands, but to millions of degrees, two to ten million. The Sun and all stars are hottest far above their surface. Why would that be?
The answer is, it’s not a campfire. It’s plasma.
If space is a sea of charged particles, then what should stars be, but massive gathering nodes for electrical current. Here’s the model: electrical lines of current in space, converging in a plasma, burst into arc mode as they concentrate on a large, central sphere. The Sun itself is an anode – not the source of energy, but a gathering point. The space around it is superheated by the convergence of plasma power lines, which burst into lightning arcs, reaching millions of degrees in the corona. The power comes from outside of the Sun. Which is why it’s cooler beneath the fire on top.
And if you don’t believe it, understand that the official story admits all of this – the Sun is hottest far above its surface. They don’t have an answer – they call it the “solar coronal heating problem.” They add it to a long list of “problems,” and keep collecting coins for their going theory. It’s gotta be rough to be a tenured academic researcher. They might as well put a sign on their clubhouse: “No new ideas allowed.”
By the way, I once overheard my uncle, the AIDS researcher, talking about places of possible employment for a Ph.D. He remarked “Well, there’s always the NIH, they never fire you.” In other words, it’s nice to guard the clubhouse. Except for the rest of us.
Electric Stars
There are two researchers who’ve done more exploration of this model than any others I know of: Ralph Juergens, who devised the electric sun model, and Wal Thornhill, who pursued and expanded it and who introduced it to readers and researchers through his incredible essays at holoscience.com. I want to thank them both and I hope you look up their work. Ralph left the Earth behind in 1979, but look up his papers, I’ll bet he’ll appreciate it.
And here it is: the electric sun. Power-lines throttle through galaxies and converge in massive star forges. They increase in size and power and attract more and more material. Their attractive force increases as the particle flow becomes denser and brighter; it begins to scavenge local materials.
As plasma researcher Wal Thornhill told me in a 2010 interview:

“As far as we can see – and when I say ‘see,’ I mean that radio telescopes are very important in the electric universe because they can detect radio waves and detect their polarization.
The polarization of the radio waves allows you to map the magnetic field directions in space. Once you’ve done that, it’s a given in plasma physics that electric currents will flow along the direction of the ambient magnetic field lines. So in other words, you can begin to trace the circuits in deep space.
We find the galaxies themselves arranged like Catherine Wheels – that’s the great spiral galaxies – along intergalactic power lines, what are called Birkeland currents. They’re like giant twisted pairs of electric currents which flow through space.
In various places, if the density of matter – the gases and dust in space – are sufficient, these pinch down. It’s called a magnetic pinch [or z-pinch]. In pinching down, they scavenge the matter from the surrounding space and squeeze it, heat it, rotate it and form the stars that we see. They do that in a particular pattern which we can reproduce in the laboratory. That pattern is the spiral galaxy.
It’s an organic picture of the universe and it’s a connected picture. We’re not isolated islands in space. Stars are not isolated, they’re connected electrically and gravitationally. It’s a completely new way of looking at our place in the universe.”

The mainstream can’t get its head out of the 17th Century to examine electricity in space, but without it, they’re lost. The attractive and explosive forces in outer space are monumental. What holds galaxies together? What energy source drives the star forges? It’s not allowed to be electricity, that’s dinged from the start. Instead, it’s left up to old Immanuel Kant, again. Yes, NASA is back in the land of gravity, doing another thought-experiment.
Learn more about electric stars and the electric universe in Chapter 9 of “Official Stories,” by Liam Scheff available now on Amazon worldwide and Createspace.
http://theintelhub.com/2012/08/30/twinkle-twinkle-electric-star/

CLIMATE HISTORY: GLOBAL WARMING SUPPLEMENTARY

PART 1

PART 2

PART 3

PART 4

 

PART 5

                                                          PART 6
                                

CLIMATE CHANGE - IS CO2 THE CAUSE?

PART 1

PART 2

PART 3

PART 4

THE GOVERNMENT PLANS TO BREAK ITS OWN CLIMATE CHANGE LAW

Politicians are finally admitting that our 'carbon' targets and our energy needs are incompatible

Ed Davey, the Liberal Democrat Energy Secretary Photo: JANE MINGAY

By Christopher Booker 28 Jul 2012

It is not often our Government lets on that it is intending to commit a very serious breach of the law – even if it does so in such opaque fashion that it hopes no one will notice. But that is what we can read between the lines of last week’s statement by Ed Davey, Secretary of State for Energy and Climate Change, which revealed just what a catastrophic shambles he is making of Britain’s energy policy.

The headlines that greeted this document were all that the spin doctors of the Department of Energy and Climate Change (DECC) could have wished for. They focused on the “victory” of Mr Davey over George Osborne, in managing to preserve the subsidy given to onshore wind turbines (currently 100 per cent) at 90 per cent, rather than the 75 per cent the Treasury supposedly wanted. The reports dutifully echoed DECC’s claim that this would bring “£25 billion of investment into the UK economy”, while Mr Davey was allowed by the Today programme to get away with the risible claim that this would “create hundreds of thousands of green jobs”.

Everything about this statement betrayed that Mr Davey and his officials have begun to realise that they are impaled on two wholly irreconcilable hooks. On one hand, they are under two legal obligations: a commitment to the EU that we will generate 32 per cent of our electricity from “renewables” by 2020; and, under the Climate Change Act, that we will cut our “carbon emissions” by 80 per cent within 40 years. On the other hand, it is their duty to ensure that we produce enough electricity to keep our lights on.

Hidden in the small print of Davey’s statement are two passages of particular significance. One, so obscurely phrased that it seems to have passed everyone by, is that by 2017 we hope to be generating “79 terawatt hours” (TWh) of electricity a year from renewables, rising by 2020 to the “108 TWh needed to meet the UK’s 2020 renewable energy target”. To make sense of this, one must look at the section of DECC’s website showing that, in 2010, the last year for which we have figures, we used 378 TWh of electricity, of which only 10 TWh, or 2.6 per cent, came from wind. Slightly more than this came from other renewables, such as hydro. But to meet that 32 per cent target within eight years, almost all the increase would have to come from new wind turbines.

If 3,000-odd turbines produced 2.6 per cent in 2010, then to meet the EU target would require something like the “32,000 turbines” mentioned by Davey’s predecessor Chris Huhne just before he resigned. This would require us to build about 10 giant turbines every day for the next eight years. Regardless of how many billions of pounds of subsidy might be thrown at this, in practical terms it is quite out of the question.

The first thing we might thus learn from Davey’s statement is that we will miss that legal target by a country mile. An even more revealing passage, however, is one that concedes that we are going to need more gas-fired power stations. Gas, says Davey, will remain “an important part of the energy mix”, not just to provide back-up for all those wind turbines when the wind isn’t blowing, but also to meet our “everyday demands” to 2030 and beyond.
It is all very well for Davey to throw in limp references to how this will “meet our carbon budget” with the aid of “carbon capture and storage”; but as he and his officials well know, piping off CO2 from power stations to bury it under the North Sea is just a pipe-dream. It is still an “unproven technology”, as Davey admits, for the simple reason that it can never be made to work.
So what we see emerging here for the first time is an official admission that, in order to keep our lights on and our economy running, we have no alternative but to rely massively on fossil-fuel gas, which will drive a coach and horses through the Climate Change Act’s target of an 80 per cent emissions cut.
Of course, the politicians will deny this, but they can only do so on the basis of wishful thinking. They are not going to get their “carbon capture” or their 32,000 wind turbines, let alone those “hundreds of thousands of green jobs”. In all directions they are screwed. And not the least telling feature of last week’s statement was that it made no reference to the shale gas revolution which has already halved US gas prices in five years, and which could solve our own energy problems by providing cheap gas for centuries.
One day we will have our shale gas and we will see the Climate Change Act repealed. These things will happen because the penny is finally dropping that the only alternative is economic suicide. But as yet, our politicians are unable to admit openly the enormity of the mess they have landed us in.
Greenland’s ice cap was on the brink of melting… for a few hours
Nothing could have better demonstrated the desperate straits to which global warmists have been driven as they try to keep their scare going than two satellite pictures in last Tuesday’s Guardian, showing a change that had come over the Greenland ice cap. One showed, in white, the second-largest mass of land ice on the planet, seemingly intact. The other, taken a few days later, showed in pink a seemingly ubiquitous melting. These Nasa pictures, we were told, showed alarmingly that, for the first time in history, the surface ice was melting right across Greenland. It took only hours for this scare story to be blown apart.
A tiny rise in air temperatures had momentarily taken them just above freezing, enough to melt a few inches of surface ice. But the ice below it, up to two miles deep, had been unaffected. This had happened before, in 1889. Ice cores show that it happens every 150 years or so. Within hours, as even the BBC admitted, the ice had frozen again. The shortest scare in history was over.

http://www.telegraph.co.uk/comment/columnists/christopherbooker/9434114/The-Government-plans-to-break-its-own-climate-change-law.html 

THE MAGIC OF CONSCIOUSNESS

Daniel Dennett is Fletcher Professor of Philosophy and Director of the Center for Cognitive Studies at Tufts University.

Here Professor Dennett lectures on the philosophical obstacles to understanding consciousness. This lecture Ignore warning includes topics covered in detail in his wonderful books "Consciousness Explained" and "Sweet Dreams: Philosophical Obstacles to a Science of Consciousness".

THE MOST ASTOUNDING FACT NEIL DE GRASSE TYSON

982.20 STARTING WITH PARTS

982.20  Starting With Parts: The Nonradial Line: Since humanity started with parallel lines, planes, and cubes, it also adopted the edge line of the square and cube as the prime unit of mensuration. This inaugurated geomathematical exploration and analysis with a part of the whole, in contradistinction to synergetics' inauguration of exploration and analysis with total Universe, within which it discovers whole conceptual systems, within which it identifies subentities always dealing with experimentally discovered and experimentally verifiable information. Though life started with whole Universe, humans happened to pick one part__the line, which was so short a section of Earth arc (and the Earth's diameter so relatively great) that they assumed the Earth-scratched-surface line to be straight. The particular line of geometrical reference humans picked happened not to be the line of most economical interattractive integrity. It was neither the radial line of radiation nor the radial line of gravity of spherical Earth. From this nonradial line of nature's event field, humans developed their formulas for calculating areas and volumes of the circle and the sphere only in relation to the cube-edge lines, developing empirically the "transcendentally irrational," ergo incommensurable, number pi (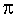), 3.14159 . . . ad infinitum, which provided practically tolerable approximations of the dimensions of circles and spheres.

982.21  Synergetics has discovered that the vectorially most economical control line of nature is in the diagonal of the cube's face and not in its edge; that this diagonal connects two spheres of the isotropic-vector-matrix field; and that those spherical centers are congruent with the two only-diagonally-interconnected corners of the cube. Recognizing that those cube-diagonal-connected spheres are members of the closest packed, allspace-coordinating, unit radius spheres field, whose radii = 1 (unity), we see that the isotropic-vector-matrix's field-occurring-cube's diagonal edge has the value. of 2, being the line interconnecting the centers of the two spheres, with each half of the line being the radius of one sphere, and each of the whole radii perpendicular to the same points of intersphere tangency.

982.30  Diagonal of Cube as Control Length: We have learned elsewhere that the sum of the second powers of the two edges of a right triangle equals the second power of the right triangle's hypotenuse; and since the hypotenuse of the two similar equiedged right triangles formed on the square face of the cube by the sphere-center-connecting diagonal has a value of two, its second power is four; therefore, half of that four is the second power of each of the equi-edges of the right triangle of the cube's diagonaled face: half of four is two.

982.31  The square root of 2 = 1.414214, ergo, the length of each of the cube's edges is 1.414214. The sqrt(2)happens to be one of those extraordinary relationships of Universe discovered by mathematics. The relationship is: the number one is to the second root of two as the second root of two is to two: 1:sqrt(2) = sqrt(2):2, which, solved, reads out as 1 : 1.414214 = 1.414214 : 2.

982.32  The cube formed by a uniform width, breadth, and height of sqrt(2) is sqrt(23), which = 2.828428. Therefore, the cube occurring in nature with the isotropic vector matrix, when conventionally calculated, has a volume of 2.828428.

982.33  This is exploratorily noteworthy because this cube, when calculated in terms of man's conventional mensuration techniques, would have had a volume of one, being the first cube to appear in the omni-geometry-coordinate isotropic vector matrix; its edge length would have been identified as the prime dimensional input with an obvious length value ofone__ergo, its volume would be one: 1 × 1 × 1 = 1. Conventionally calculated, this cube with a volume of one, and an edge length of one, would have had a face diagonal length of sqrt(2), which equals 1.414214. Obviously, the use of the diagonal of the cube's face as the control length results in a much higher volume than when conventionally evaluated.

982.40  Tetrahedron and Synergetics Constant: And now comes the big surprise, for we find that the cube as coordinately reoccurring in the isotropic vector matrix__as most economically structured by nature__has a volume of three in synergetics' vector- edged, structural-system-evaluated geometry, wherein the basic structural system of Universe, the tetrahedron, has a volume of one.

982.41  A necklace-edged cube has no structural integrity. A tension-linked, edge- strutted cube collapses.

982.42  To have its cubical conformation structurally (triangulated) guaranteed (see Secs. 615 and 740), the regular equiangled tetrahedron must be inserted into the cube, with the tetrahedron's six edges congruent with each of the six vacant but omnitriangulatable diagonals of the cube's six square faces.

982.43  As we learn elsewhere (Secs. 415.22 and 990), the tetrahedron is not only the basic structural system of Universe, ergo, of synergetic geometry, but it is also the quantum of nuclear physics and is, ipso facto, exclusively identifiable as the unit of volume; ergo, tetrahedron volume equals one. We also learned in the sections referred to above that the volume of the octahedron is exactly four when the volume of the tetrahedron of the unit-vector edges of the isotropic-vector-matrix edge is one, and that four Eighth-Octahedra are asymmetrical tetrahedra with an equiangular triangular base, three apex angles of 90 degrees, and six lower-comer angles of 45 degrees each; each of the 1/8th octahedron's asymmetric tetrahedra has a volumetric value of one-half unity (the regular tetrahedron). When four of the Eighth-Octahedrons are equiangle-face added to the equiangled, equiedged faces of the tetrahedra, they produce the minimum cube, which, having the tetrahedron at its heart with a volume of one, has in addition four one-half unity volumed Eighth-Octahedra, which add two volumetric units on its corners. Therefore, 2 + 1 = 3 = the volume of the cube. The cube is volume three where the tetrahedron's volume is one, and the octahedron's volume is four, and the cube's diagonally structured faces have a diagonal length of one basic system vector of the isotropic vector matrix. (See Illus. 463.01.)

982.44  Therefore the edge of the cube = sqrt(1/2).

982.45  Humanity's conventional mensuration cube with a volume of one turns out in energetic reality to have a conventionally calculated volume of 2.828428, but this same cube in the relative-energy volume hierarchy of synergetics has a volume of 3. 3 --------- 2.828428 = 1.06066

982.46  To correct 2.828428 to read 3, we multiply 2.828428 by the synergetics conversion constant 1.06066. (See Chart 963.10.)

982.47  Next we discover, as the charts at Secs. 963.10 and 223.64 show, that of the inventory of well-known symmetrical polyhedra of geometry, all but the cube have irrational values as calculated in the XYZ rectilinear-coordinate system__"cubism" is a convenient term__in which the cube's edge and volume are both given the prime mensuration initiating value of one. When, however, we multiply all these irrational values of the Platonic polyhedra by the synergetic conversion constant, 1.06066, all these values become unitarily or combinedly rational, and their low first-four-prime-number- accommodation values correspond exactly with those of the synergetic hierarchy of geometric polyhedra, based on the tetrahedron as constituting volumetric unity.

982.48  All but the icosahedron and its "wife," the pentagonal dodecahedron, prove to be volumetrically rational. However, as the tables show, the icosahedron and the vector-edged cube are combiningly rational and together have the rational value of three to the third power, i.e., 27. We speak of the pentagonal dodecahedron as the icosahedron's wife because it simply outlines the surface-area domains of the 12 vertexes of the icosahedron by joining together the centers of area of the icosahedron's 20 faces. When the pentagonal dodecahedron is vectorially constructed with flexible tendon joints connecting its 30 edge struts, it collapses, for, having no triangles, it has no structural integrity. This is the same behavior as that of a cube constructed in the same flexible- tendon-vertex manner. Neither the cube nor the pentagonal dodecahedron is scientifically classifiable as a structure or as a structural system (see Sec. 604).

982.50  Initial Four-Dimensional Modelability: The modelability of the XYZ coordinate system is limited to rectilinear-frame-of-reference definition of all special-case experience patternings, and it is dimensionally sized by arbitrary, e.g., c.gt.s.-system, subdivisioning increments. The initial increments are taken locally along infinitely extensible lines always parallel to the three sets of rectilinearly interrelated edges of the cube. Any one of the cube's edges may become the one-dimensional module starting reference for initiating the mensuration of experience in the conventional, elementary, energetical7 school curriculum. (Footnote 7: Energetical is in contradistinction to synergetical. Energetics employs isolation of special cases of our total experience, the better to discern unique behaviors of parts undiscernible and unmeasurable in total experience.)

982.51  The XYZ cube has no initially moduled, vertex-defined nucleus; nor has it any inherent, common, most-economically-distanced, uniform, in-out-and- circumferentially-around, corner-cutting operational interlinkage, uniformly moduled coordinatability. Nor has it any initial, ergo inherent, time-weight-energy-(as mass charge or EMF) expressibility. Nor has it any omni-intertransformability other than that of vari- sized cubism. The XYZ exploratory coordination inherently commences differentially, i.e., with partial system consideration. Consider the three-dimensional, weightless, timeless, temperatureless volume often manifest in irrational fraction increments, the general reality impoverishments of which required the marriage of the XYZ system with the c.gt.s. system in what resembles more of an added partnership than an integration of the two.

982.52  The synergetics coordinate system's initial modelability accommodates four dimensions and is operationally developable by frequency modulation to accommodate fifth- and sixth-dimensional conceptual-model accountability. Synergetics is initially nuclear-vertexed by the vector equilibrium and has initial in-out-and-around, diagonaling, and diametrically opposite, omni-shortest-distance interconnections that accommodate commonly uniform wavilinear vectors. The synergetics system expresses divergent radiational and convergent gravitational, omnidirectional wavelength and frequency propagation in one operational field. As an initial operational vector system, its (mass x velocity) vectors possess all the unique, special-case, time, weight, energy (as mass charge or EMF) expressibilities. Synergetics' isotropic vector matrix inherently accommodates maximally economic, omniuniform intertransformability.

982.53  In the synergetics' four-, five-, and six-dimensionally coordinate system's operational field the linear increment modulatability and modelability is the isotropic vector matrix's vector, with which the edges of the co-occurring tetrahedra and octahedra are omnicongruent; while only the face diagonals__and not the edges__of the inherently co-occurring cubes are congruent with the matrix vectors. Synergetics' exploratory coordination inherently commences integrally, i.e., with whole-systems consideration. Consider the one-dimensional linear values derived from the initially stated whole system, six-dimensional, omnirational unity; any linear value therefrom derived can be holistically attuned by unlimited frequency and one-to-one, coordinated, wavelength modulatability. To convert the XYZ system's cubical values to the synergetics' values, the mathematical constants are linearly derived from the mathematical ratios existing between the tetrahedron's edges and the cube's corner-to-opposite-corner distance relationships; while the planar area relationships are derived from the mathematical ratios existing between cubical-edged square areas and cubical-face-diagonaled-edged triangular areas; and the volumetric value mathematical relationships are derived from ratios existing between (a) the cube-edge-referenced third power of the-often odd-fractioned-edge measurements (metric or inches) of cubically shaped volumes and (b) the cube-face-diagonal-vector- referenced third power of exclusively whole number vector, frequency modulated, tetrahedrally shaped volumes. (See Sec. 463 and 464 for exposition of the diagonal of the cube as a wave-propagation model.)

982.54  The mathematical constants for conversion of the linear, areal, and volumetric values of the XYZ system to those of the synergetics system derive from the synergetics constant (1.060660). (See Sec. 963.10 and Chart 963.12.) The conversion constants are as follows: First Dimension: The first dimensional cube-edge-to-cube-face-diagonal vector conversion constant from XYZ to synergetics is as 1:1.060660. Second Dimension: The two-dimensional linear input of vector vs. cube-edged referenced, triangular vs. square area product identity is 1.0606602 = 1.125 = 1 1/8th = 9/8ths. The second-power value of the vector, 9/8, is in one-to-one correspondence with "congruence in modulo nine" arithmetic (see Secs. 1221.18 and 1221.20); ergo is congruent with wave-quanta modulation (see Secs. 1222 and 1223). Third Dimension: The three-dimensional of the cube-edge vs. vector-edged tetrahedron vs. cube volumetric identity is 1.0606603 = 1.192.

982.55  To establish a numerical value for the sphere, we must employ the synergetics constant for cubical third-power volumetric value conversion of the vector equilibrium with the sphere of radius 1. Taking the vector equilibrium at the initial phase (zero frequency, which is unity-two diameter: ergo unity-one radius) with the sphere of radius l; i.e., with the external vertexes of the vector equilibrium congruent with the surface of the sphere = 4/3 pi () multiplied by the third power of the radius. Radius = 1. 13 = 1. l × 1.333 × 3.14159 = 4.188. 4.188 times synergetics third-power constant 1.192 = 5 = volume of the sphere. The volume of the radius 1 vector equilibrium = 2.5. VE sphere = 2 VE.

982.56  We can assume that when the sphere radius is 1 (the same as the nuclear vector equilibrium) the Basic Disequilibrium 120 LCD tetrahedral components of mild off- sizing are also truly of the same volumetric quanta value as the A and B Quanta Modules; they would be shortened in overall greatest length while being fractionally fattened at their smallest-triangular-face end, i.e., at the outer spherical surface end of the 120 LCD asymmetric tetrahedra. This uniform volume can be maintained (as we have seen in Sec. 961.40).

982.57  Because of the fundamental 120-module identity of the nuclear sphere of radius 1 (F = 0), we may now identify the spherical icosahedron of radius 1 as five; or as 40 when frequency is 2F2. Since 40 is also the volume of the F2 vector-equilibrium- vertexes-congruent sphere, the unaberrated vector equilibrium F2 = 20 (i.e., 8 × 2 1/2 nuclear-sphere's inscribed vector equilibrium). We may thus assume that the spherical icosahedron also subsides by loss of half its volume to a size at which its volume is also 20, as has been manifested by its prime number five, indistinguishable from the vector equilibrium in all of its topological hierarchies characteristics.

Fig. 982.58

982.58  Neither the planar-faceted exterior edges of the icosahedron nor its radius remain the same as that of the vector equilibrium, which, in transforming from the vector equilibrium conformation to the icosahedral state__as witnessed in the jitterbugging (see Sec. 465) __did so by transforming its outer edge lengths as well as its radius. This phenomenon could be analagous the disappearance of the nuclear sphere, which is apparently permitted by the export of its volume equally to the 12 surrounding spheres whose increased diameters would occasion the increased sizing of the icosahedron to maintain the volume 20-ness of the vector equilibrium. This supports the working assumption that the 120 LCD asymmetric tetrahedral volumes are quantitatively equal to the A or B Quanta Modules, being only a mild variation of shape. This effect is confirmed by the discovery that 15 of the 120 LCD Spherical Triangles equally and interiorly subdivide each of the eight spherical octahedron's triangular surfaces, which spherical octahedron is described by the three-great-circle set of the 25 great circles of the spherical vector equilibrium.

982.59  We may also assume that the pentagonal-faced dodecahedron, which is developed on exactly the same spherical icosahedron, is also another transformation of the same module quantation as that of the icosahedron's and the vector equilibrium's prime number five topological identity.

982.60  Without any further developmental use of pi () we may now state in relation to the isotropic vector matrix synergetic system, that: The volume of the sphere is a priori always quantitatively: __ 5F3 as volumetrically referenced to the regular tetrahedron (as volume = 1); or __ 120F3 as referenced to the A and B Quanta Modules.

Fig. 982.61

982.61  There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres, each of a tetra volume of five; i.e., of 120 A and B Quanta Modules omniembracing our hierarchy of nuclear event patternings. See Illus. 982.61 in the color section, which depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order whole number, equilibrious state of the micro-macro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially- rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualizable only in its equilibrious state.

982.61A  Cosmic Hierarchy of Omnidirectionally-phased Nuclear-centered, Convergently-divergently Intertransformable Systems: There is realized herewith a succession of concentric, 12-around-one, closest-packed spheres omniembracing our hierarchy of nuclear event patternings. The synergetics poster in color plate 9 depicts the synergetics isometric of the isotropic vector matrix and its omnirational, low-order-whole- number, equilibrious state of the macro-micro cosmic limits of nuclearly unique, symmetrical morphological relativity in their interquantation, intertransformative, intertransactive, expansive-contractive, axially rotative, operational field. This may come to be identified as the unified field, which, as an operationally transformable complex, is conceptualized only in its equilibrious state.

982.62  Table of Concentric, 12-Around-One, Closest-Packed Spheres, Each of a Tetra Volume of Five, i.e., 120 A and B Quanta Modules, Omniembracing Our Hierarchy of Nuclear Event Patternings. (See also Illus. 982.61 in drawings section.) Symmetrical Form: Tetra Volumes A and B Quanta Modules F2 Sphere 40 960 F2 Cube 24 576 F2 Vector equilibrium 20 480 F0 Rhombic dodecahedron 6 144 F0 Sphere (nuclear) 5 120 F0 Octahedron 4 96 F0 Cube 3 72 F0 Vector equilibrium 2½ 60 F0 Tetrahedron 1 24 F0 Skew-aberrated, disequilibrious icosahedron 5 120 F2 Skew-aberrated, disequilibrious icosahedron 40 960

982.62A  Table of Concentric, 12-around-one, Closest-packed Spheres Omniembracing Our Hierarchy of Nuclear Event Patternings (Revised): Symmetrical Form: Tetravolumes A and B Quanta Modules F0 Tetrahedron 1 24 F0 Vector equilibrium 2.5 60 F0 Double-Tet cube 3 72 F0 Octahedron 4 96 F0 Rhombic triacontahedron* 5+ 120+ F0 Rhombic dodecahedron 6 144 F2 Vector equilibrium 20 480 F2 Double-Tet cube 24 576 * The spheric spin domain of the rhombic triacontahedron "sphere."

982.63  Sphere and Vector Equilibrium: Sphere = vector equilibrium in combined four-dimensional orbit and axial spin. Its 12 vertexes describing six great circles and six axes. All 25 great circles circling while spinning on one axis produce a spin-profiling of a superficially perfect sphere.

982.64  The vector equilibrium also has 25 great circles (see Sec. 450.10), of which 12 circles have 12 axes of spin, four great circles have four axes of spin, six great circles have six axes of spin, and three great circles have three axes of spin. (12 + 4 + 6 + 3 = 25)

982.65  Vector equilibrium = sphere at equilibrious, ergo zero energized, ergo unorbited and unspun state.

982.70  Hierarchy of Concentric Symmetrical Geometries: It being experimentally demonstrable that the number of A and B Quanta Modules per tetrahedron is 24 (see Sec.942.10); that the number of quanta modules of all the symmetric polyhedra congruently co-occurring within the isotropic vector matrix is always 24 times their whole regular-tetrahedral-volume values; that we find the volume of the nuclear sphere to be five (it has a volumetric equivalence of 120 A and B Quanta Modules); that the common prime number fivetopological and quanta-module value identifies both the vector equilibrium and icosahedron (despite their exclusively unique morphologies__see Sec. 905, especially 905.55; that the icosahedron is one of the three-and-only prime structural systems of Universe (see Secs. 610.20 and 1011.30) while the vector equilibrium is unstable__because equilibrious__and is not a structure; that their quanta modules are of equal value though dissimilar in shape; and that though the vector equilibrium may be allspace-fillingly associated with tetrahedra and octahedra, the icosahedron can never be allspace-fillingly compounded either with itself nor with any other polyhedron: these considerations all suggest the relationship of the neutron and the proton for, as with the latter, the icosahedron and vector equilibrium are interexchangingly transformable through their common spherical-state omnicongruence, quantitatively as well as morphologically.

982.71  The significance of this unified field as defining and embracing the minimum- maximum limits of the inherent nuclear domain limits is demonstrated by the nucleus- concentric, symmetrical, geometrical hierarchy wherein the rhombic dodecahedron represents the smallest, omnisymmetrical, selfpacking, allspace-filling, six-tetra-volume, uniquely exclusive, cosmic domain of each and every closest-packed, unit-radius sphere. Any of the closest-packed, unit-radius spheres, when surrounded in closest packing by 12 other such spheres, becomes the nuclear sphere, to become uniquely embraced by four successive layers of surrounding, closest-packed, unit-radius spheres__each of which four layers is uniquely related to that nucleus__with each additional layer beyond four becoming duplicatingly repetitive of the pattern of unique surroundment of the originally unique, first four, concentric-layered, nuclear set. It is impressive that the unique nuclear domain of the rhombic dodecahedron with a volume of six contains within itself and in nuclear concentric array: __ the unity-one-radiused sphere of volume five; __ the octahedron of volume four; __ the cube of volume three; __ the prime vector equilibrium of volume 2 l/2; and __ the two regular (positive and negative) tetrahedra of volume one each. This succession of 1, 2, 3, 4, 5, 6 rational volume relationships embraces the first four prime numbers 1, 2, 3, and 5. (See Illus. 982.61 in color section.) The volume-24 (tetra) cube is thelargest omnisymmetrical self-packing, allspace-filling polyhedron that exactly identifies the unique domain of the original 12-around-one, nuclear-initiating, closest packing of unit-radius spheres. The unit quantum leap of 1__going to 2__going to 3__going to 4__going to 5__going to 6, with no step greater than 1, suggests a unique relationship of this set of six with the sixness of degrees of freedom.8 (Footnote 8: For further suggestions of the relationship between the rhombic dodecahedron and the degrees of freedom see Sec. 426 537.10 954.47.)

982.72  The domain limits of the hierarchy of concentric, symmetrical geometries also suggests the synergetic surprise of two balls having only one interrelationship; while three balls have three__easily predictable__relationships; whereas the simplest, ergo prime, structural system of Universe defined exclusively by four balls has an unpredictable (based on previous experience) sixness of fundamental interrelationships represented by the six edge vectors of the tetrahedron.

982.73  The one-quantum "leap" is also manifest when one vector edge of the volume 4 octahedron is rotated 90 degrees by disconnecting two of its ends and reconnecting them with the next set of vertexes occurring at 90 degrees from the previously interconnected-with vertexes, transforming the same unit-length, 12-vector structuring from the octahedron to the first three-triple-bonded-together (face-to-face) tetrahedra of the tetrahelix of the DNA-RNA formulation. One 90-degree vector reorientation in the complex alters the volume from exactly 4 to exactly 3. This relationship of one quantum disappearance coincident to the transformation of the nuclear symmetrical octahedron into the asymmetrical initiation of the DNA-RNA helix is a reminder of the disappearing-quanta behavior of the always integrally end-cohered jitterbugging transformational stages from the 20 tetrahedral volumes of the vector equilibrium to the octahedron's 4 and thence to the tetrahedron's 1 volume. All of these stages are rationally concentric in our unified operational field of 12-around-one closest- packed spheres that is only conceptual as equilibrious. We note also that per each sphere space between closest-packed spheres is a volume of exactly one tetrahedron: 6 - 5 = 1.

---

Copyright © 1997 Estate of R. Buckminster Fuller

http://www.rwgrayprojects.com/synergetics/s09/p8220.html